A Proof About Roses

A proof about roses? Who would have thought!

In this case, a rose is a shape generated in a polar graph from the equation

$$r = A\cos(n \theta + \phi)$$

graphed in the domain $[0, 2\pi]$.

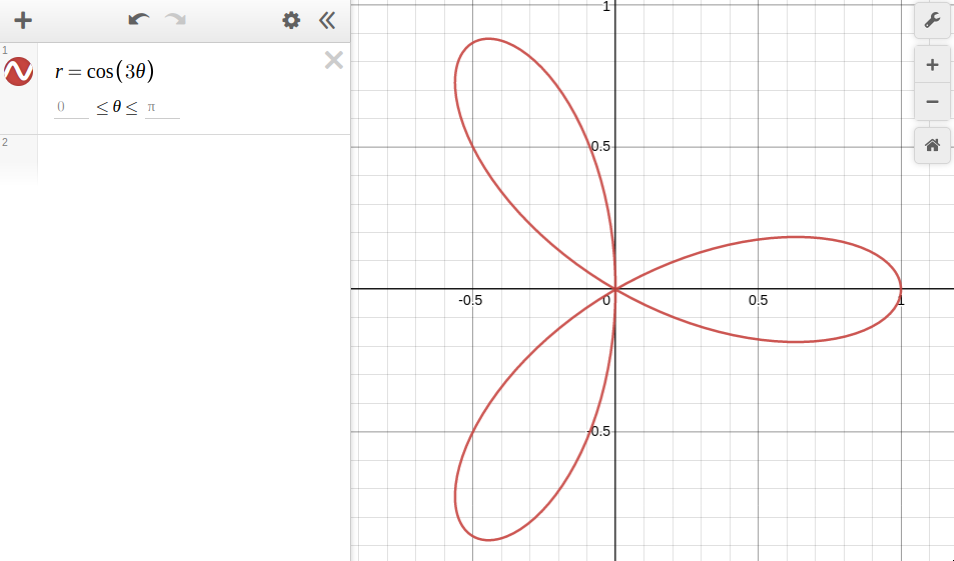
However, something peculiar happens when you change the coefficient to $\theta$ ($n$).

When $n$ is even, $2n$ petals are produced. On the other hand, when it is odd, $n$ petals are produced (after $\pi$, the petals go back over on themselves)!

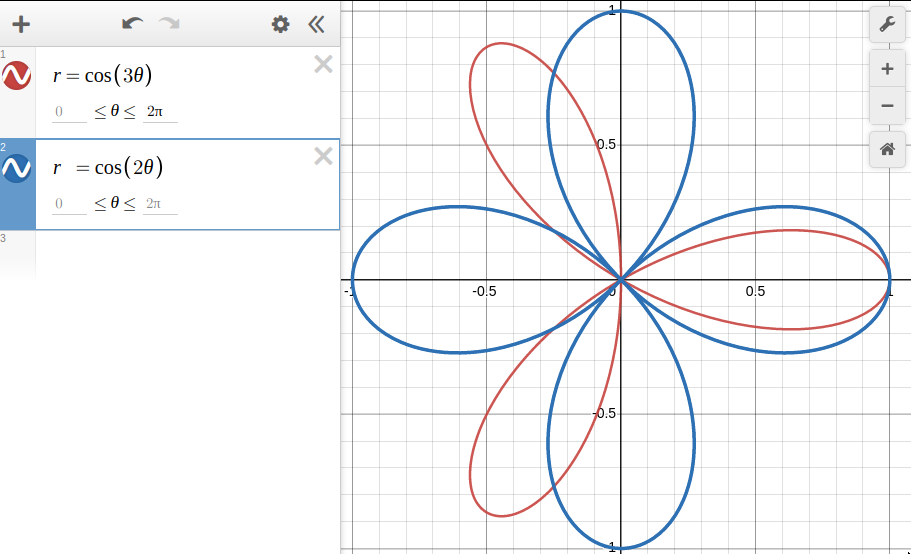
My teacher said that there were proofs, but they involved calculus, so naturally I took it upon myself as a challenge to prove it without calculus!

The Proof Follows:

Assume for the proof that $n \in \text{the set of all odd numbers}$.

At $\pi$, $\cos(n\theta)$ will always be $-1$, while $\cos(2n\theta)$ will always be 1.

Proving the above statement will allow us to conclude the proof.

Recall the function for period of a sinusoidal: the period of a function of the form $\cos(mx)$ is $\text{period} = \frac{2\pi}{m}$. Rearranging this with some algebra, we get $m = \frac{2\pi}{\text{period}}$. At $2\pi$, $m$ periods will have been completed, so it follows that at $\pi$, $m/2$ periods will have been completed. If $m$ is an odd number, as it is in our case, then the amount of periods completed at $\pi$ will have a fractional component of $1/2$. When the amount of periods completed has a fractional component of $1/2$, in a regular cosine curve, it means that the function output must be $-1$ because that is the value of cosine at half a cycle.

Conversely, we can prove that where the coefficient is even, in the case of $\cos(2n\theta)$, the output at $\pi$ must be $1$ with the same logic. At $\pi$, $2n/2 = n$ periods have been completed, which means that the value must be the same as the start of a cycle in a cose graph which is $1$.

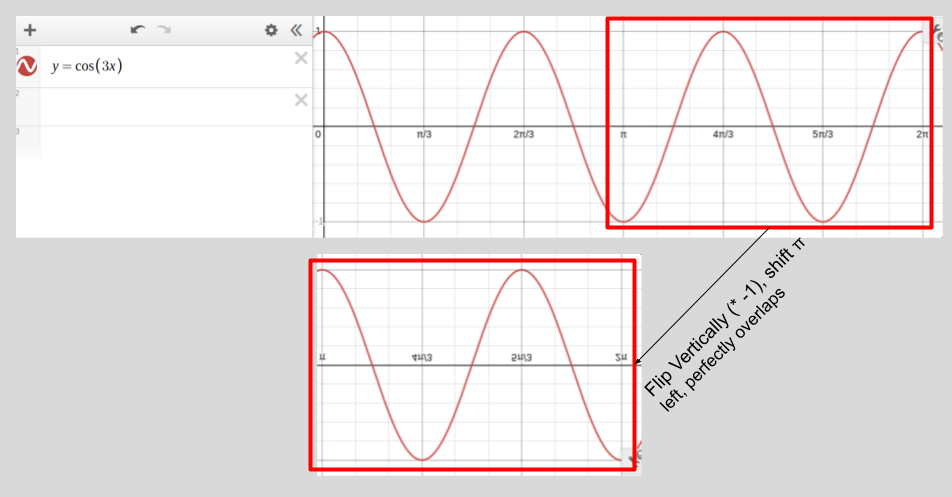
Okay, we have now established this, but how does it help us? Recall that in a polar graph, negating the radius is the same as adding $\pi$ to $\theta$. Adding $\pi$ to a cosine graph will shift it left by $\pi$. So for any polar graph, taking the graph from $[\pi, 2\pi]$, multiplying it by -1, and translating it to the domain $[0, \pi]$ will produce the exact same graph. Since a graph in the second half of a period, when we multiply $\theta$ by an odd number, from $[\pi, 2\pi]$, is $-1$ times the graph in the first half of the period (because the periods are exactly $1/2$ period out of sync), when you shift left and multiply the graph by $-1$, it overlaps perfectly with the graph from $[0, \pi]$! This causes there to be no new petals drawn.

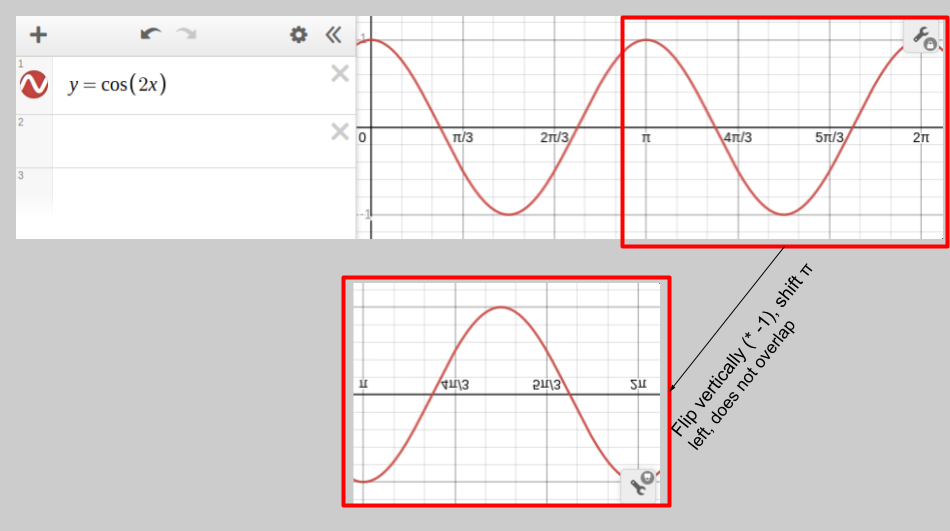
And since multiplying $\theta$ by an even coefficient leaves it at the start of a cycle at $\pi$, it does not overlap on itself when multiplied by $-1$ and shifted by $\pi$ to the left. This causes new petals to be drawn where they don’t overlap.

Check out these examples for visual intuition (pay attention to graph label numbers: they are flipped):

QED!!!