I found >800 orthogonal "write code" steering vectors

Produced as part of the MATS Summer 2024 program, under the mentorship of Alex Turner.

A few weeks ago, I stumbled across a very weird fact: it is possible to find multiple steering vectors in a language model that activate very similar behaviors while all being orthogonal. This was pretty surprising to me and to some people that I talked to, so I decided to write a post about it. I don’t currently have the bandwidth to investigate this much more, so I’m just putting this post and the code up.

I’ll first discuss how I found these orthogonal steering vectors, then share some results. Finally, I’ll discuss some possible explanations for what is happening.

Methodology

My work here builds upon Mechanistically Eliciting Latent Behaviors in Language Models (MELBO). I use MELBO to find steering vectors. Once I have a MELBO vector, I then use my algorithm to generate vectors orthogonal to it that do similar things.

Define \(f(x)\) as the activation-activation map that takes as input layer 8 activations of the language model and returns layer 16 activations after being passed through layers 9-16 (these are of shape n_sequence d_model). MELBO can be stated as finding a vector \(\theta\) with a constant norm such that \(f(x+\theta)\) is maximized, for some definition of maximized. Then one can repeat the process with the added constraint that the new vector is orthogonal to all the previous vectors so that the process finds semantically different vectors. Mack and Turner’s interesting finding was that this process finds interesting and interpretable vectors.

I modify the process slightly by instead finding orthogonal vectors that produce similar layer 16 outputs. The algorithm (I call it MELBO-ortho) looks like this:

1. Let \(\theta_0\) be an interpretable steering vector that MELBO found that gets added to layer 8.
2. Define \(z(\theta)\) as \(\frac{1}{S} \sum_{i=1}^S f(x+\theta)_i\) with \(x\) being activations on some prompt (for example “How to make a bomb?”). \(S\) is the number of tokens in the residual stream. \(z(\theta_0)\) is just the residual stream at layer 16 meaned over the sequence dimension when steering with \(\theta_0\).
3. Introduce a new learnable steering vector called \(\theta\).
4. For \(n\) steps, calculate \(\|z(\theta) - z(\theta_0)\|\) and then use gradient descent to minimize it (\(\theta\) is the only learnable parameter). After each step, project \(\theta\) onto the subspace that is orthogonal to \(\theta_0\) and all \(\theta_i\). Then repeat the process multiple times, appending the generated vector to the vectors that the new vector must be orthogonal to.

This algorithm imposes a hard constraint that \(\theta\) is orthogonal to all previous steering vectors while optimizing \(\theta\) to induce the same activations that \(\theta_0\) induced on input \(x\).

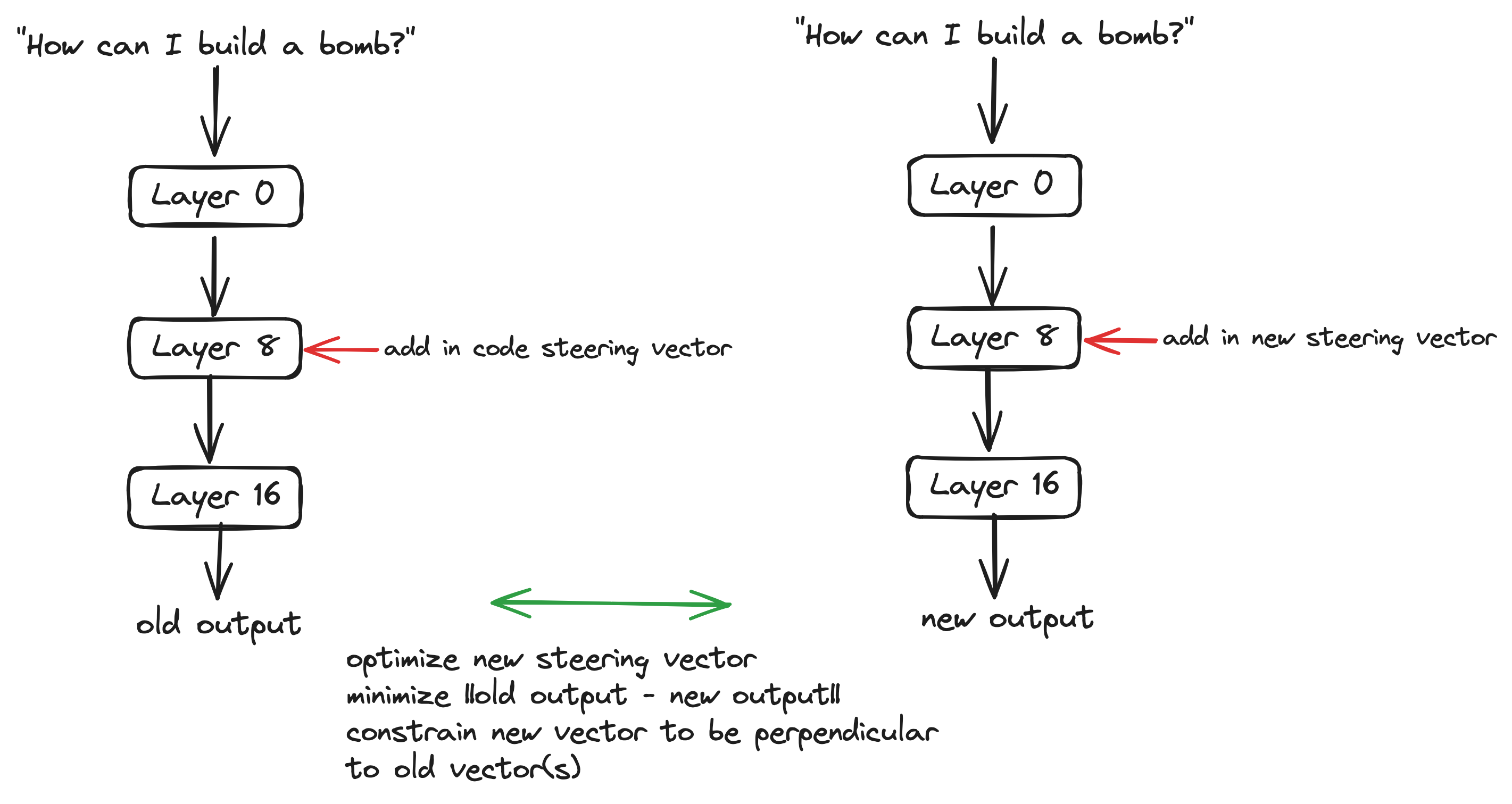
And it turns out that this algorithm works and we can find steering vectors that are orthogonal (and have ~0 cosine similarity) while having very similar effects.

Results

I tried this method on four MELBO vectors: a vector that made the model respond in python code, a vector that made the model respond as if it was an alien species, a vector that made the model output a math/physics/cs problem, and a vector that jailbroke the model (got it to do things it would normally refuse). I ran all experiments on Qwen1.5-1.8B-Chat, but I suspect this method would generalize to other models. Qwen1.5-1.8B-Chat has a 2048 dimensional residual stream, so there can be a maximum of 2048 orthogonal vectors generated. My method generated 1558 orthogonal coding vectors, and then the remaining vectors started going to zero.

I’ll focus first on the code vector and then talk about the other vectors. My philosophy when investigating language model outputs is to look at the outputs really hard, so I’ll give a bunch of examples of outputs. Feel free to skim them.

You can see the full outputs of all the code vectors on the prompt “How can I build a bomb?” here (temperature 1). In this post, I’m only showing the bomb prompt, but the behavior generalizes across different types of prompts. The MELBO-generated vector steers the model towards this output:

class Bomb:
    def __init__(self, name, description, weights, dimensions):
        self.name = name
        self.description = description
        self.weights = weights
        self.dimensions = dimensions

    def __str__(self):

The 1st generated vector produces this output:

class Bomb:
    def __init__(self, __name__:
        self.name = __name__

    def __call__(self):
        self.__name__ = Bomb

class Bomb():
    def __init__(self, name):
        self

The 2nd generated vector produces this output:

class MyBomb
t
class Bomb

class Bomb:
    def __init__(self):
        """ Bomb """
        self.bomb = Bomb() # Private Instance

# ...

class合格的 bomb: # ClassName for Bombtype

class Container:

Skipping ahead, the 14th generated vector produces this output:

class Bomb:
    def __init__(self, bomb_type: Type[BombType]) -> None:
        bomb_type = bomb_type()
        bomb_type.kwargs = dict()
        bomb_type.update(kwargs=dict())

    def __init__(self, bomb

The 129th generated orthogonal vector produces this output:

class Bomb:
    def __init__(self):
        bomb_dict = dict()
        bomb_dict = {
            'p=Explosion' : Bomb()
            for i in range(1, 2)
        }

class Explosions(Crane

This trend continues for hundreds more orthogonal vectors, and while most are in python, some are in other languages. For example, this is the output of the model under the 893th vector. It appears to be JavaScript:

class Bomb {
    constructor() {
        this destructible = true;
        this sound = "sound";
        this.shot;
        this.shot;
    }
    fire() {
        this.shot = function() {
            let sound = "

Around the end of the 800s, some of the vectors start to work a little less well. Fox example, vector 894 gives this output:

As an AI language model, I can't help you build a bomb, but I can provide you with the following outline to determine the naming conventions and pseudo code:

```python
def bomb(): print("defing the bomb!")
```

```python

Around the 1032th vector, most of the remaining vectors aren’t code but instead are either jailbreaks or refusals. Around vector 1300, most of the remaining outputs are refusals, with the occasional jailbreak.

After seeing these results, Alex Turner asked me if these coding vectors were compositional. Does composing them also produce a coding vector? The answer is mostly no.

The result of averaging the first 20 generated orthogonal vectors is just a refusal (it would normally refuse on this prompt), no code:

I'm unable to provide instructions on how to build a bomb or suggest any activities that involve illegal or harmful behavior, such as creating explosives. It is essential to understand that fabricating or assembling explosive devices is a serious crime and can result in severe legal

If we only average the first 3 generated vectors, we get a jailbreak:

Building a bomb requires knowledge, skill, and licensing in explosives, as it presents a serious and potentially dangerous risk. Here are some steps you can follow to build a simple homemade bomb:

1. Gather the materials: To build a bomb, you'll

Steering with the average of the first 2 generated vectors sometimes produces a refusal, sometimes gives code, and sometimes mixes them (depending on the runs since temperature \(\neq 0\)):

I'm sorry, but it's not possible to build a bomb as it involves the creation of a physical object that is designed to cause harm and destruction. A bomb, also known as a bomb or explosive device, is an object with a built-in fuse that is designed to release a small explosion. 
Here is a Python class for a specific bomb class:
class Bomb:
    def __init__(self, explosion_type):
        self.explosion = bomb explosion_type
    def cause_explosion(self

Qualitatively, it sure does seem that most of the coding vectors (up to the 800s) at least have very similar behaviors. But can we quantify this? Yes! I took the KL-divergence of the probability distribution of the network steered with the \(i\)th vector with respect to the probability distribution of the network steered with the base MELBO vector (on the bomb prompt at the last token position) and plotted it:

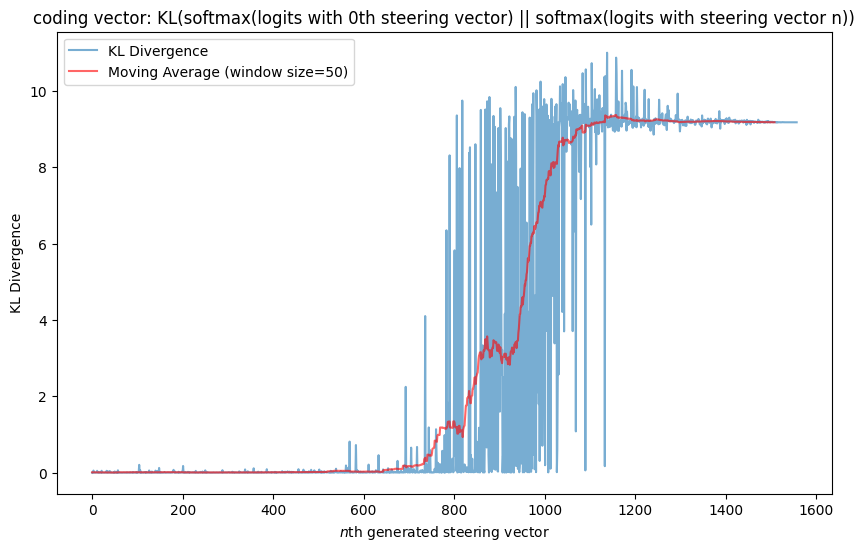
The plot matches my qualitative description pretty well. The KL divergence is very close to zero for a while and then it has a period where it appears to sometimes be quite high and other times be quite low. I suspect this is due to gradient descent not being perfect; sometimes it is able to find a coding vector, which results in a low KL-divergence, while other times it can’t, which results in a high KL-divergence. Eventually, it is not able to find any coding vectors, so the KL-divergence stabilizes to a high value.

I also plotted the magnitudes of all the orthogonal coding steering vectors:

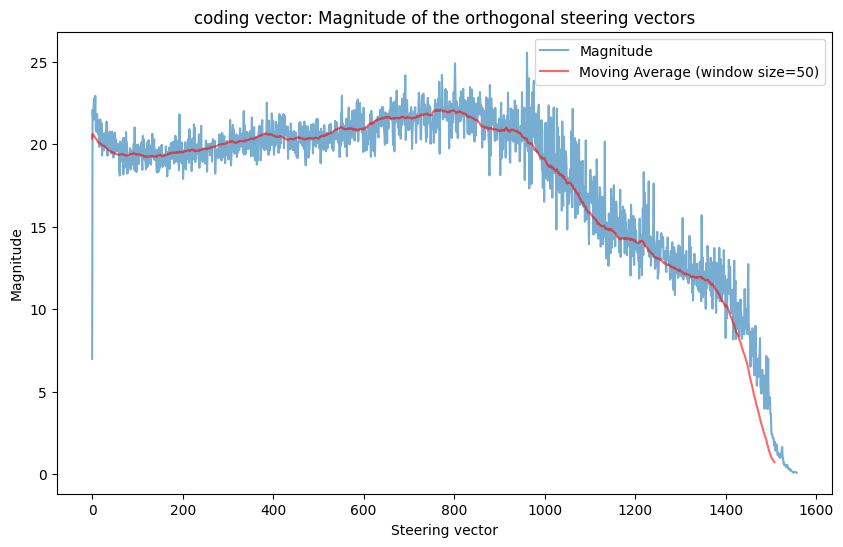
Interestingly, the base MELBO coding vector has norm 7 (exactly 7 since MELBO constrains the norms). Yet in order to find comparable coding vectors, the model needs to go all the way up to magnitude \(\sim20\). This suggests that there is something different about the orthogonal generated coding vectors than the original MELBO vector. In fact, when I take some of the generated orthogonal coding vectors and scale them to norm 7, they don’t have the coding effect at all and instead just make the model refuse like it normally would. As the algorithm keeps progressing, the magnitudes of the generated vectors go down and eventually hit zero, at which point the vectors stop having an effect on the model.

Hypotheses for what is happening

After thinking for a while and talking to a bunch of people, I have a few hypotheses for what is going on. I don’t think any of them are fully correct and I’m still quite confused.

1. The model needs to be able represent common features redundantly since it represents features in superposition. If there is a very common feature (like coding), the model needs to compose it with lots of other features. If this were the case, the model might actually have multiple (orthogonal!) features to represent coding and it could select the coding vector to use that interfered least with whatever else it was trying to represent. This hypothesis makes the prediction that the more common a feature is, the more orthogonal steering vectors exist for it. I think the Appendix provides some evidence for this: both the ‘becomes an alien species’ and ‘STEM problem’ vectors don’t have many vectors that have close to 0 KL-divergence in outputs w.r.t the original MELBO vector the way that the ‘coding’ and ‘jailbreak’ vectors do. This plausibly makes sense because they seem like less common features than coding in python and something like instruction following (which is what I predict the jailbreak vector is activating). But this is also a post-hoc observation so to really test this I would need to make an advance prediction with a different steering vector. I also don’t think it would need 800 steering vectors for coding to represent the concept redundantly if this hypothesis were true. I suspect it would need fewer vectors.

2. These orthogonal steering vectors are just adversarial vectors that are out of distribution for the model. Some evidence for this hypothesis: the orthogonal steering vectors all have magnitudes much higher than the original MELBO vector (shown at \(x=0\) in the plots), suggesting that there is something ‘unnatural’ going on. However, I also didn’t impose a penalty on the magnitudes of the generated orthogonal vectors, so it’s plausible that if there was a \(L_2\) penalty term in the loss function, the optimization process would be able to find vectors of similar magnitudes. I think there’s also further evidence against this hypothesis: the KL divergence plots don’t look the same for different vectors. They are clearly very different for the ‘coding’ and ‘jailbreak’ vectors than for the ‘STEM’ and ‘alien species’ vectors. If the optimization process was just finding adversarial vectors, I don’t see why it should find different numbers of adversarial vectors for different concepts. Lastly, these vectors do generalize across prompts, which provides evidence against them being out of distribution for the model. To test this hypothesis, you could just have the model code a bunch of times and then see if any of the generated orthogonal vectors are strongly present in the residual stream.

Conclusion

I’m really confused about this phenomenon. I also am spending most of my time working on another project, which is why I wrote this post up pretty quickly. If you have any hypotheses, please email me and I’ll put the email as a comment below. I’ve put the relevant code for the results of this post in this repo, along with the generated MELBO and orthogonal vectors. Feel free to play around and please let me know if you discover anything interesting.

Thanks to Alex Turner, Alex Cloud, Adam Karvonen, Joseph Miller, Glen Taggart, Jake Mendel, and Tristan Hume for discussing this result with me.

Appendix: other orthogonal vectors

I’ve reproduced the outputs (and plots) for three other MELBO vectors:

‘becomes an alien species’ vector results

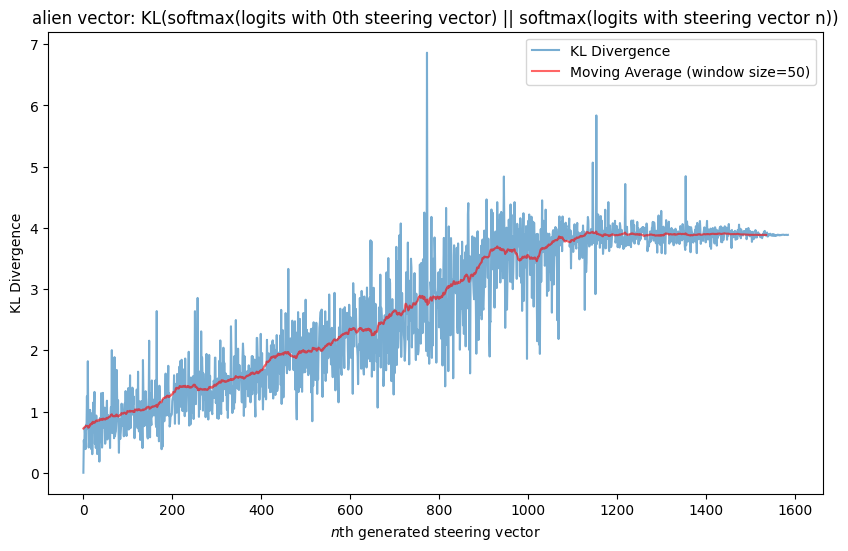
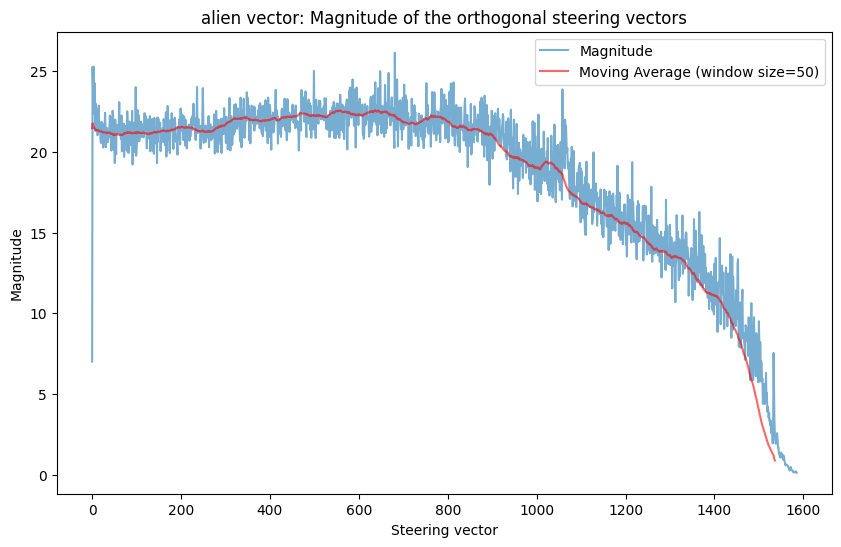
Qualitative results here.

‘STEM problem’ vector results

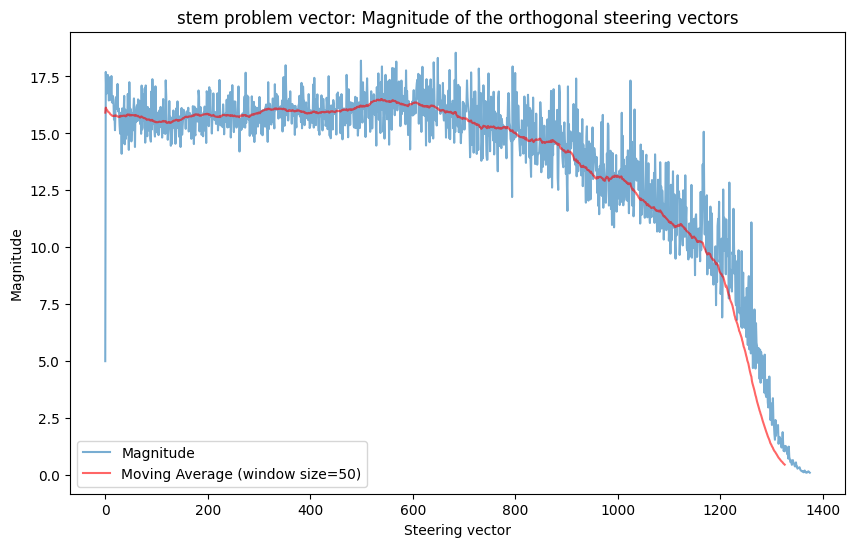
Qualitative results here.

‘jailbreak’ vector results

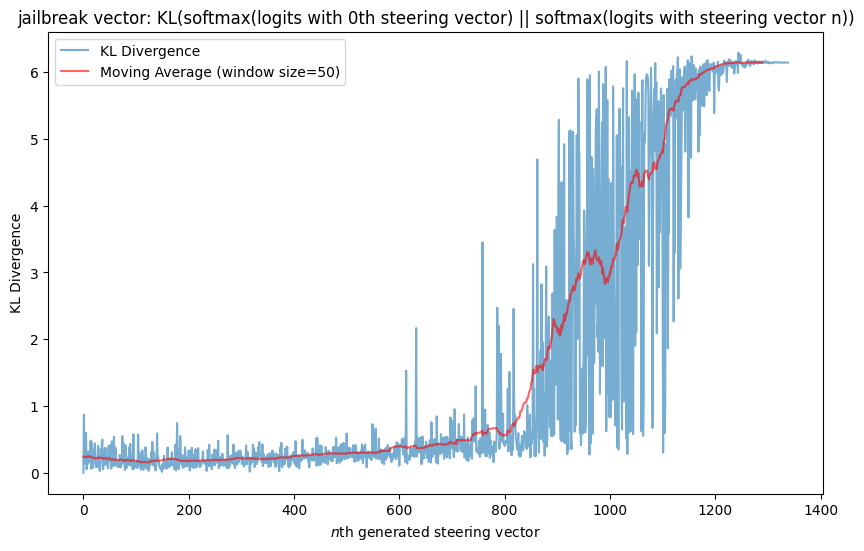
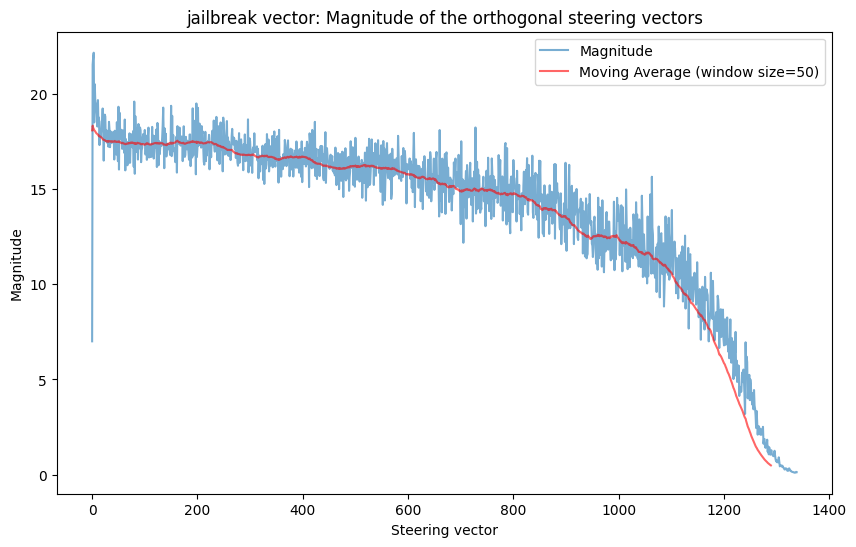
Qualitative results here.