Building intuition with spaced repetition systems
Do you ever go to a lecture, follow it thinking it makes total sense, then look back at your notes later and realize it makes no sense? This used to happen to me, but I’ve learned how to use spaced repetition to fully avoid this if I want. I’m going to try to convey this method in this post.
Much of my understanding of how to create flashcards comes from “Using spaced repetition systems to see through a piece of mathematics” by Michael Nielsen and “How to write good prompts: using spaced repetition to create understanding” by Andy Matuschak, but I think my method falls in between both, in terms of abstraction. Finally, I want to credit Quantum Country for being an amazing example of flashcards created to develop intuition in users.
My method is more abstract than Michael Nielsen’s approach, since it does not only apply to mathematics, but to any subject. Yet it is less abstract than Andy Matuschak’s approach because I specifically use it for ‘academic subjects’ that require deep intuition of (causal or other) relationships between concepts. Many of Matuschak’s principles in his essay apply here (I want to make sure to give him credit), but I’m looking at it through the ‘how can we develop deep intuition in an academic subject in the fastest possible time?’ lens.
Minimize Inferential Distance on Flashcards
A method that I like to repeat to myself while making flashcards that I haven’t seen in other places is that each flashcard should only have one inferential step on it. I’m using ‘inferential step’ here to mean a step such as remembering a fact, making a logical deduction, visualizing something, or anything that requires thinking. It’s necessary that a flashcard only have a single inferential step on it. Anki trains the mind to do these steps. If you learn all the inferential steps, you will be able to fully re-create any mathematical deduction, historical story, or scientific argument. Knowing (and continually remembering) the full story with spaced repetition builds intuition.
I’m going to illustrate this point by sharing some flashcards that I made while trying to understand how Transformers (GPT-2) worked. I made these flashcards while implementing a transformer based on Neel Nanda’s tutorials and these two blog posts.
Understanding Attention
The first step in my method is to learn or read enough so that you have part of the whole loaded into your head. For me, this looked like picking the attention step of a transformer and then reading about it in the two blog posts and watching the section of the video on it. It’s really important to learn about something from multiple perspectives. Even when I’m making flashcards from a lecture, I have my web browser open and I’m looking up things that I thought were confusing while making flashcards.
My next step is to understand that intuition is fake! Really good resources make you feel like you understand something, but to actually understand something, you need to engage with it. This engagement can take many forms. For technical topics, it usually looks like solving problems or coding, and this is good! I did this for transformers! But I also wanted to not forget it long term, so I used spaced repetition to cement my intuition.
Enough talk, here are some flashcards about attention in a transformer. For each flashcard, I’ll explain why I made it. Feel free to scroll through.

I start with a distillation of the key points of the article.

I wanted to make sure that I knew what the attention operation was actually doing, as the blog posts emphasized this.

When building intuition, I find it helpful to know “the shape” or constraints about something so that I can build a more accurate mental model. In this case, this card helped me visualize some sort of probability distribution when thinking about attention.
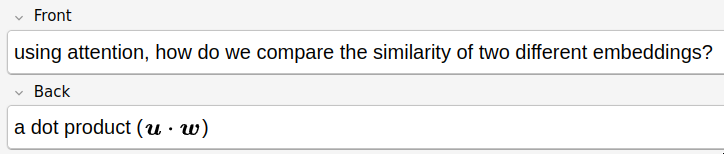
This was really useful since it connected to some of my previous cards about (cosine) similarity. I was able to put attention in the context of just comparing vectors for similarity, which made it feel much more real to me.
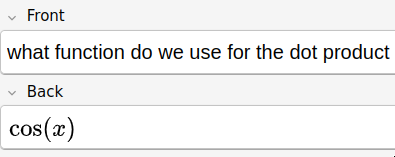
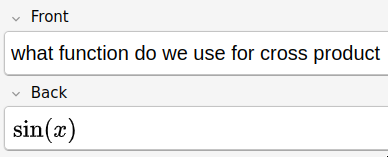
I wrote these after realizing that I would often get dot and cross product mixed up and wanted to stop. Sometimes, even small things like this have a big impact on my intuition. I knew I needed to get the basics right.

I included this because I was slowly building up to the general formula for attention, piece by piece. I knew I needed to understand how attention worked at a low level to gain intuition for it. Just carding the formula wouldn’t work.
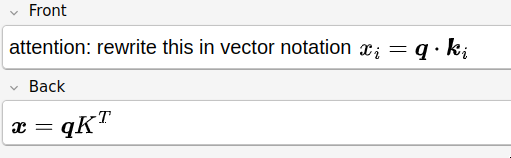
I wanted to make sure that I understood where the \(K\) matrix was coming from.

Again, this is slowly building up to the general attention formula. I made myself generalize from the previous flashcard to this one (vectorized version). It’s really important to have multiple flashcards point at the same topic in slightly different ways to gain intuition.
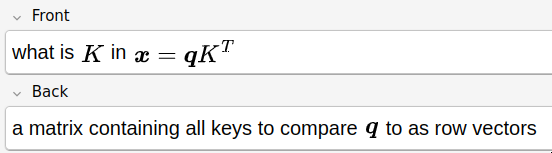
I wanted to fully understand this version of the formula, so I made myself know all the parts.

To go even deeper, I wanted to visualize the shapes of the matrices because I felt that would help me gain intuition, so I did that on this flashcard.
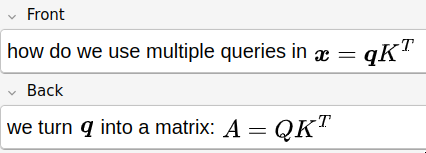
Next, I was still working my way towards the general attention formula, so I asked myself to vectorize it even more. Now I had a path towards \(A\)
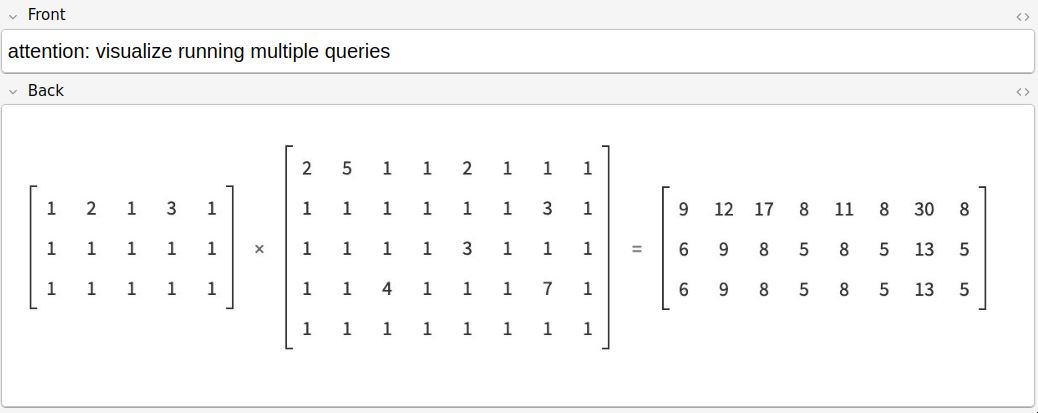
I needed to visualize this of course.

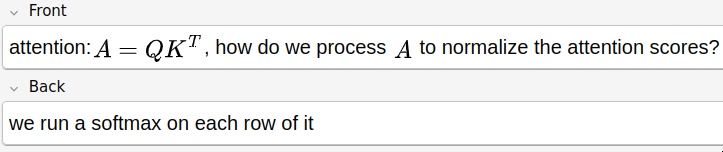
I made this flashcard to remind myself that we need to normalize attention scores with softmax. The visual aid helps because it showed me the shape of the previous computation, so I could visually see that the vectors on the right should be normalized. I had a flashcard above that said that attention scores need to be normalized (\(\sum_i a_i = 1\)), so I built on that. I’ve found that interconnected flashcards build intuition best.
Now I generalized the softmax to the vectorized version of attention with multiple queries. This generalization is important to help me build intuition.

Now I’m finally adding the intuition for the rest of the attention formula.

Finally! The full attention formula! It’s glorius and I understand every part of it.

I add this one in to make sure I get intuition for why we scale. If I was making this card again, I would actually make two. This one would be a verbal explanation and then another card would ask me to explain the nonlinearity with a numerical example.
I have more flashcards about attention, but I’m going to stop here because I feel these are fairly complete and self-contained (I go more into linear algebra that I needed to brush up on and self-attention).
After doing these flashcards, I have significantly more intuition for how attention in Transformers works! I could explain it to someone with little preparation and derive it from first principles.
I hope you’ve enjoyed reading this, and I hope that it will help you make better flashcards in the future.
If you have any thoughts on this method, please reach out at jacoblevgw at gmail dot com.
I’m considering live-streaming (or just making a video) of myself doing this on a totally new topic to show how I do this in real-time, since it works so well for me. Let me know if you think this could be helpful.